Termodinamika adalah cabang ilmu Fisika yang membahas tentang hubungan antara panas (kalor) dan usaha yang dilakukan oleh kalor tersebut. Dalam melakukan pengamatan mengenai aliran energi antara panas dan usaha ini dikenal dua istilah, yaitu sistem dan lingkungan. Apakah yang dimaksud sistem dan lingkungan dalam termodinamika? Untuk memahami penggunaan kedua istilah tersebut dalam termodinamika, perhatikanlah Gambar 1. berikut.
 |
| Gambar 1. Bola besi dan air merupakan sistem yang diamati. Adapun, udara luar merupakan lingkungannya. |
Misalkan, Anda mengamati aliran kalor antara bola besi panas dan air dingin. Ketika bola besi tersebut dimasukkan ke dalam air. Bola besi dan air disebut sistem karena kedua benda tersebut menjadi objek pengamatan dan perhatian Anda. Adapun, wadah air dan udara luar disebut lingkungan karena berada di luar sistem, tetapi dapat memengaruhi sistem tersebut. Dalam pembahasan termodinamika, besaran yang digunakan adalah besaran makroskopis suatu sistem, yaitu tekanan, suhu, volume, entropi, kalor, usaha, dan energi dalam.
Usaha yang dilakukan oleh sistem (gas) terhadap lingkungannya bergantung pada proses -proses dalam termodinamika, di antaranya proses isobarik, isokhorik, isotermal, dan adiabatik.
1. Usaha Sistem terhadap Lingkungannya
Pada pembahasan Bab sebelumnya, Anda telah mempelajari definisi usaha (W) yang dilakukan pada benda tegar, yaitu
W = F x s
Bagaimanakah cara menghitung usaha pada gas? Tinjaulah suatu gas yang berada dalam tabung dengan penutup berbentuk piston yang dapat bergerak bebas, seperti terlihat pada Gambar 2.
 |
| Gambar 2. Ketika gas ideal di dalam tabung dipanaskan,gas tersebut memuai sehingga piston berpindah sejauh Δs. |
Ketika gas tersebut dipanaskan, piston akan berpindah sejauh Δs karena gas di dalam tabung memuai dari volume awal V1 menjadi volume akhir V2. Gaya yang bekerja pada piston adalah F = pA. Jika luas penampang piston (A) dan tekanan gas dalam tabung (P) berada dalam keadaan konstan, usaha yang dilakukan oleh gas dinyatakan dengan persamaan
W = pA Δs
Oleh karena A Δs = ΔV, persamaan usaha yang dilakukan gas dapat ditulis menjadi :
W = p ΔV (1–1)
atau
W = p(V2 – V1) (1–2)
dengan:
p = tekanan gas (N/m2),
ΔV = perubahan volume (m3), dan
W = usaha yang dilakukan gas (joule).
Nilai W dapat berharga positif atau negatif bergantung pada ketentuan berikut.
a. Jika gas memuai sehingga perubahan volumenya berharga positif, gas (sistem) tersebut dikatakan melakukan usaha yang menyebabkan volumenya bertambah. Dengan demikian, usaha W sistem berharga positif.
b. Jika gas dimampatkan atau ditekan sehingga perubahan volumenya berharga negatif, pada gas (sistem) diberikan usaha yang menyebabkan volume sistem berkurang. Dengan demikian, usaha W pada tersebut sistem ini bernilai negatif.
Usaha yang dilakukan oleh sistem dapat ditentukan melalui metode grafik. Pada Gambar 3a dapat dilihat bahwa proses bergerak ke arah kanan (gas memuai). Hal ini berarti V2 > V1 atau ΔV > 0 sehingga W bernilai positif (gas melakukan usaha terhadap lingkungan). W sama dengan luas daerah di bawah kurva yang diarsir (luas daerah di bawah kurva p –V dengan batas volume awal dan volume akhir)
Selanjutnya perhatikan Gambar 3b. Jika proses bergerak ke arah kiri (gas memampat), V2 < V1 atau ΔV < 0 sehingga W bernilai negatif (lingkungan melakukan usaha terhadap gas). W = – luas daerah di bawah kurva p–V yang diarsir.
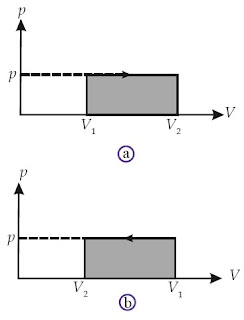 |
| Gambar 3. (a) Grafik P–V suatu gas yang mengalami pemuaian (melakukan ekspansi) (b) Grafik P–V suatu gas yang mengalami pemampatan (diberi kompresi) |
Cobalah Anda tinjau kembali Persamaan (1–1). Dari persamaan tersebut dan grafik hubungan tekanan (p) terhadap (V) pada Gambar 3, Anda dapat menyimpulkan bahwa suatu sistem dikatakan melakukan usaha (W berharga positif) atau sistem diberi usaha (W berharga negatif), jika pada sistem tersebut terjadi perubahan volume ( ΔV).
Contoh Soal 1 :
Tentukanlah usaha yang dilakukan gas. (1 atm = 105 N/m2)
Kunci Jawaban :
Diketahui: p = 2 atm, V1 = 0,3 L, dan V2 = 0,5 L.
1 liter = 1 dm3 = 10–3 m3
W = p ( ΔV) = p (V2 – V1)
W = 2 × 105 N/m2 (0,5 L – 0,2 L) × 10–3 m3 = 60 Joule.
Contoh Soal 2 :
Gambar berikut menunjukkan suatu siklus termodinamika dari suatu gas ideal.
Tentukanlah usaha yang dilakukan gas:
Tentukanlah usaha yang dilakukan gas:
a. dari keadaan A ke B,
b. dari B ke C,
c. dari C ke D,
d. dari D ke A, dan
e. dari A kembali ke A melalui B, C, dan D
Kunci Jawaban :
Diketahui: p = pB = 2 N/m2, pD = pC = 1 N/m2, VA = VD = 2 m3, dan VB = VC = 3 m3.
a. WAB = p (VB – VA) = (2 × 105 N/m2) (3 – 2) × 10–3 m3 = 200 joule
b. WBC = p (VC – VB) = 0
c. WCD= p (VD – VC) = (1 × 105 N/m2) (2 – 3) × 10–3 m3 = -100 joule
d. WDA= p (VA – VD) = 0
e. WABCDA = Wsiklus = 200 Joule + 0 – 100 Joule + 0 = 100 joule
selain itu, dapat ditentukan dengan cara :
WABCDA = Wsiklus = luas arsiran
WABCDA = (2 – 1) × 105 N/m2(3 – 2) × 10–3 m3
WABCDA = 100 joule.2. Proses dalam Termodinamika
Terdapat empat proses dalam gas pada bahasan termodinamika. Pada pembahasan Bab 8, Anda telah mengenal tiga proses, yaitu isotermal, isobarik, dan isokhorik. Proses yang keempat adalah proses adiabatik. Usaha yang terdapat pada gas yang mengalami proses-proses termodinamika tersebut akan diuraikan sebagai berikut.
a. Proses Isotermal
Proses isotermal adalah suatu proses perubahan keadaan gas pada suhu tetap.
Menurut Hukum Boyle, proses isotermal dapat dinyatakan dengan persamaan :
 |
| Gambar 4. A–B merupakan proses isotermal. |
pV = konstan
atau
p1V1 = p2V2
Dalam proses ini, tekanan dan volume sistem berubah sehingga persamaan W = p ΔV tidak dapat langsung digunakan. Untuk menghitung usaha sistem dalam proses isotermal ini digunakan cara integral. Misalkan, pada sistem terjadi perubahan yang sangat kecil sehingga persamaan usahanya dapat dituliskan sebagai
dW = pdV (1–3)
Jika Persamaan (1–3) diintegralkan maka dapat dituliskan :
ò dW = ò pdV
Dari persamaan keadaan gas ideal diketahui bahwa p = nRT/V. Oleh karena itu, integral dari Persamaan (9–3) dapat dituliskan menjadi :
ò dW = ò (nRT / V)
Jika konstanta n R, dan besaran suhu (T) yang nilainya tetap dikeluarkan dari integral, akan diperoleh :
W = nR T (lnV2 – lnV1)
W = n RT ln (V2/V1)
atau
Contoh Soal 3 :
Sepuluh mol gas helium memuai secara isotermal pada suhu 47 °C sehingga volumenya menjadi dua kali volume mula-mula. Tentukanlah usaha yang dilakukan oleh gas helium.
Kunci Jawaban :
Diketahui: T = 47 °C = (47 + 273) K = 320 K dan V2 = 2V1.
Usaha yang dilakukan gas pada proses isotermal:
W = n RT ln (V2/V1) = (10 mol) ( 8,31 J/mol)(320 K) ln (2V2/V1) = 26.592 ln 2 = 18.428 joule
b. Proses Isokhorik
Proses isokhorik adalah suatu proses perubahan keadaan gas pada volume tetap.
Menurut Hukum Gay-Lussac proses isokhorik pada gas dapat dinyatakan dengan persamaan :
 |
| Gambar 5. A–B merupakan proses isokhorik. |
p/T = konstan
atau
p1/T1 = p2/T2
Oleh karena perubahan volume dalam proses isokhorik ΔV = 0 maka usahanya W = 0.
c. Proses Isobarik
Proses isobarik adalah suatu proses perubahan keadaan gas pada tekanan tetap.
Menurut Hukum Charles, persamaan keadaan gas pada proses isobarik dinyatakan dengan persamaan :
 |
| Gambar 6. C–D adalah proses isobarik. |
V/T = konstan
atau
V1/T1 = V2/T2
Oleh karena volume sistem berubah, sedangkan tekanannya tetap, usaha yang dilakukan oleh sistem dinyatakan dengan persamaan
W = pΔV = p (V2 – V1) (1–5)
Contoh Soal 4 :
Suatu gas yang volumenya 1,2 liter perlahan-lahan dipanaskan pada tekanan tetap 1,5 × 105 N/m2 hingga volumenya menjadi 2 liter. Berapakah usaha yang dilakukan gas?
Kunci Jawaban :
Kunci Jawaban :
Diketahui: V1 = 1,2 L, V2 = 2 L, dan p = 1,5 × 105 N/m2.
Usaha yang dilakukan gas pada tekanan tetap (isobarik) adalah
W = p (V2 – V1) = (1,5 × 105 N/m2) (2 – 1,2) × 10–3 m3 = 120 joule
Contoh Soal 5 :
Tentukanlah:
a. usaha gas dari A ke B,
b. usaha gas dari B ke C,
c. usaha gas dari C ke A, dan
d. usaha netto gas dalam satu siklus.
Kunci Jawaban :
Diketahui: pA = pB = 3 × 105 Pa, pC = 1 × 105 Pa, VA = 2 L, dan VB = VC = 6 L.
a. Proses A ke B adalah proses isobarik. Usaha dari A ke B dapat dihitung dengan
persamaan
WAB = p(VB – VA)
WAB = 3 × 105 Pa (6 – 2) × 10–3 m3 = 1.200 jouleb. Proses B ke C adalah proses isokhorik. Oleh karena VC = VB, usaha yang dilakukan gas WBC = 0
c. Proses dari C ke A adalah isotermal. Oleh karena pC:VC = pA:VA, usaha dari C ke A adalah :
WCA = nRT ln (VA/VC) = pCVC ln (VA/VC) = pAVA ln (VA/VC) (ingat: pV = nRT)
d. Usaha netto gas dalam satu siklus ABCA :
Wsiklus = WAB + WBC + WCA = 1.200 joule + 0 + (–415,8 joule) = 784,2 joule
d. Proses Adiabatik
Proses adiabatik adalah suatu proses perubahan keadaan gas di mana tidak ada kalor (Q) yang masuk atau keluar dari sistem (gas). Proses ini dapat dilakukan dengan cara mengisolasi sistem menggunakan bahan yang tidak mudah menghantarkan kalor atau disebut juga bahan adiabatik. Adapun, bahan-bahan yang bersifat mudah menghantarkan kalor disebut bahan diatermik
Proses adiabatik ini mengikuti persamaan Poisson sebagai berikut
p Vγ = konstan
atau
p1 V1γ = p2 V2γ (1–6)
Oleh karena persamaan gas ideal dinyatakan sebagai pV = nRT maka Persamaan (9–4) dapat ditulis :
T1V1(γ –1) = T2 V2(γ –1) (1–7)
dengan γ = CP/CV = konstanta Laplace, dan CP/CV > 1. CP adalah kapasitas kalor gas pada tekanan tetap dan CV adalah kalor gas pada volume tetap. Perhatikan diagram p – V pada Gambar 7.
Dari kurva hubungan p – V tersebut, Anda dapat mengetahui bahwa:
 |
| Gambar 7. Pada proses adiabatik, kurva p–V lebih curam dibandingkan dengan kurva p–V pada proses isotermal. |
1) Kurva proses adiabatik lebih curam daripada kurva proses isotermal.
2) Suhu, tekanan, maupun volume pada proses adiabatik tidak tetap.
Oleh karena sistem tidak melepaskan atau menerima kalor, pada kalor sistem proses adiabatik Q sama dengan nol. Dengan demikian, usaha yang dilakukan oleh sistem hanya mengubah energi dalam sistem tersebut. Besarnya usaha pada proses adiabatik tersebut dinyatakan dengan persamaan berikut.
W= 3/2 nRT−T = 3/2 (p1 V1 − p2 V2) (1–8)
Catatan Fisika :
OTEC (Ocean Thermal Energy Conversion) adalah sebuah pembangkit tenaga listrik mini. Mesin ini bekerja berdasarkan perbedaan suhu antara permukaan laut yang hangat dan kedalaman laut yang dingin. Pusat pembangkit listrik ini bebas polusi.
Contoh Soal 6 :
OTEC
 |
| OTEC di Hawai. [2] |
Contoh Soal 6 :
Sebuah mesin memiliki rasio pemampatan 12 : 1 yang berarti bahwa setelah pemampatan, volume gas menjadi 1/12 volume awalnya. Anggap bahan bakar bercampur udara pada suhu 35 °C, tekanan 1 atm, dan γ = 1,4. Jika proses pemampatan terjadi secara adiabatik, hitunglah tekanan pada keadaan akhir dan suhu campuran.
Kunci Jawaban :
Diketahui: V2 = 1/12 V1, T1 = 35 + 273 = 308 K, dan p1 = 1 atm.
Untuk menentukan tekanan akhir p2, gunakan rumus :
p2 = 32,4 atm.
Suhu campuran atau suhu akhir T2 diperoleh sebagai berikut :
Suhu campuran atau suhu akhir T2 diperoleh sebagai berikut :
T2 = 308 K (12)1,4 – 1 = 308 K (12)0,4 = 832 K = 559 °C
Contoh Soal 7 :
Usaha sebesar 2 × 103 J diberikan secara adiabatik untuk memampatkan 0,5 mol gas ideal monoatomik sehingga suhu mutlaknya menjadi 2 kali semula. Jika konstanta umum gas R = 8,31 J/mol K, tentukanlah suhu awal gas.
Kunci Jawaban :
Diketahui: W = 2 × 103 J, T2 = 2T1, dan n = 0,5 mol.
T1 = 2W / 3nR = 2(2 x 103 joule) / 3 x 0,5 mol x 8,31 J/molK = 321 K
W = 3/2 n R (T2 – T1) = 3/2 n R (2T1 – T1)
W = 3/2 n R T1
Jadi, suhu awal gas adalah 321 K.




Tidak ada komentar:
Posting Komentar